足して2で割るだけじゃない!? もうひとつの平均“相乗平均”を理解しよう!

こんにちは!ライターの小林です。
いきなりですが、問題です。
以下に、A町~C町の人口データがあります。
平均値をお答えください。
| まち | 人口 |
|---|---|
| A町 | 10万人 |
| B町 | 20万人 |
| C町 | 15万人 |
答えは簡単、15万人ですね。
さすがに間違えた人はいなかったでしょう!
続いて、こちらはどうでしょう。
例えばある基準年から見た、ある地区の人口増加率です。
3年間の人口増加率の平均はいくつでしょうか?
| 年 | 人口増加率(対前年比) |
|---|---|
| 1年目 | 1.1倍 |
| 2年目 | 1.9倍 |
| 3年目 | 1.5倍 |
答えは・・・1.5倍?
そう回答されたあなた! この続きを見て私と一緒に勉強しましょう!
「足して割る」だけが平均値ではないのです。
変化率など、掛け算の場合の平均“相乗平均”!
足して、足した数で割る平均には名前があり、「相加平均(算術平均)」と言います。
一般的な平均といったらコレですね。説明不要です。
一方、今回の“人口増加率”のように、一定期間の変化率等の平均を求めるためには、
「相乗平均(幾何平均)」を使います。
計算の数式はこちら。
数式を見て脱落しないでくださいね。
なぜ掛けてルートにすると平均になるのか?
例題で順番に考えます。
下の図のように、基準値χが、α1倍、α2倍、α3倍していくと、χ3になることが分かっています。
χをA倍するとχ3になることも併せて考えます。
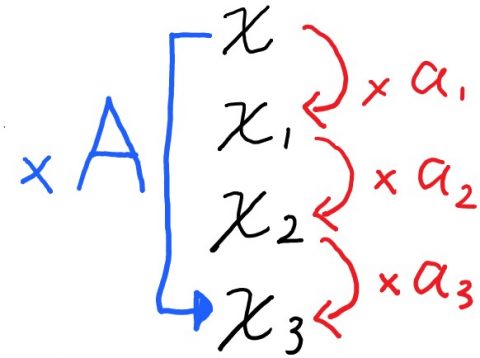
α1、α2、α3は、それぞれχの変化率だと考えるとイメージしやすいかもしれません。
ここで気付くと思いますが、【×A】と【×α1×α2×α3】倍は同じであることが分かりますね。
数式にするとこんな感じ。
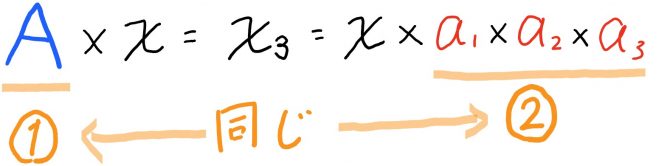
両辺とも①と②に【χ】をかけているだけなので、答えは同じはずですね。
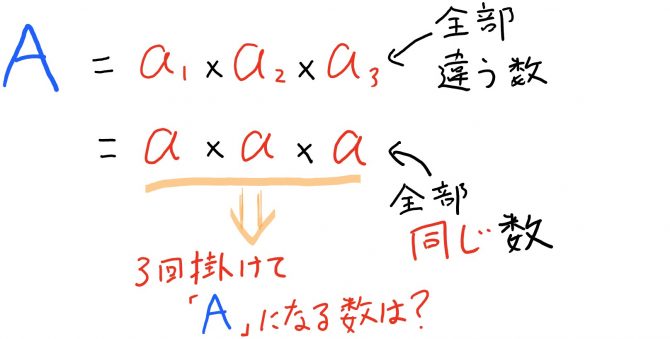
今、②のα1とα2、α3はそれぞれ違う数字を仮定しています。
この平均を考えるためには、
どのような同じ値を3回掛ければ【A】になるのか?を考えればいいことになります!
ルート(√)の復習
ちょっと寄り道してルート(√)の復習です。
√100の答えは分かりますか?
正解は【10】ですね。
頭の中でどんな計算をしましたか?
「えーっと、同じ数同士を掛けて(2乗して)【100】になる数だから・・・」
おそらくこんな感じでしょう。
2乗したらある値になるもの、
これを√で表記するということでした。
3乗したらある値になるもの、これも√で表現できることを覚えていますか?
表記はこんな感じ。

これは、3乗したら8になる数を表現しています。
答えは2ですね。
※n乗してAになる数を【Aのn乗根】と言います。
詳しく知りたい方は“累乗根”で調べてみてくださいね。
累積根は掛け算の平均値!
・・・・ところで、勘の良い方は気付いたでしょうか?
「いったい何のこと?」という方、
この数式をみて何か気付きませんか。
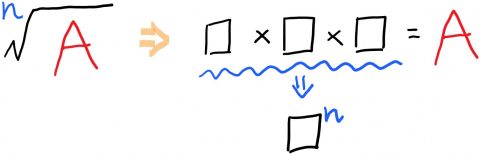
そう!
Aのn乗根とは「どのような同じ値をn回掛ければAになるのか」という考え方でした!
先ほど残した課題、
「どのような同じ値を3回掛ければ【A】になるか」と同じですね。
つまり、掛け合わせた合計数値の累乗根が、掛け算の場合の平均
= “相乗平均”というわけです。
もう一度先ほどの相乗平均の数式を見てみましょう。
今度はすんなり受け入れられるのではないでしょうか。
変化率の平均値の計算、もう間違えませんね。
答え合わせ!
さて、 最初に出した例題を考えて見ましょう。
| 年 | 人口増加率(対前年比) |
|---|---|
| 1年目 | 1.1倍 |
| 2年目 | 1.9倍 |
| 3年目 | 1.5倍 |
この表の“相乗平均”を計算すると、【1.463….】が導き出されます。
※ExcelではGEOMEAN関数で相乗平均が計算できます。
たとえば基準の数値を1,000として、この増加率を当てはめてみましょう。
そのうえで、相加平均と相乗平均の結果を比較してみます。
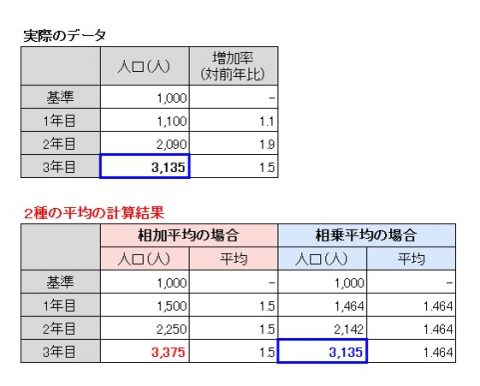
3年目の数値は、相加平均ではなく相乗平均が見事に一致します。
これまでの内容を理解された方なら、当たり前の結果であることがわかりますよね。
安易に相加平均をしてしまうと、相乗平均より大きな数値になってしまうので注意が必要です。
まとめ
今日は、慣れ親しんだ平均とは違う“相乗平均”を勉強しました。
実はその他にも、いろんな平均があります。
速さの平均などで使われる“調和平均”、集団ごとの人数差を考慮する“加重平均” など。
正確なデータ分析のためには平均一つとっても注意しないといけませんね。
文系の私は、統計・数学は日々勉強です。
悩める文系の皆様!いっしょにがんばりましょう!
この記事を書いた人

小林 寿名古屋事務所 企画課
専門統計調査士、MUDアドバイザー 主に市町村の社会調査・計画策定コンサルティングに従事 データビジュアライゼーションやオープンデータ利活用が得意分野
