クロス集計だけでものを言うのは危ない!~知っておきたいクロス集計の基礎知識②~
こんにちは、ライターの田原です。
今回は、クロス集計で知っておきたいことの第2弾です。(前回記事『クロス集計は正しく読まなと危ない!~知っておきたいクロス集計の基礎知識①~』はこちらです!)
クロス集計については、書きたいことがたくさんあるのですが、その中でも僕が重要だと思うことを発信していきたいと思います。
カイ二乗検定
今回は、クロス集計とは切っても切れないカイ2乗検定についてです。
でも、今回はカイ2乗検定のやり方!というようなことは書きません。
インターネットで「カイ2乗検定」と調べれば、カイ2乗検定の方法や理論など詳しく情報が出てきますし、本屋に行けば「エクセルでできるカイ2乗検定!」みたいなレベルの本もたくさんありますので、そちらで調べてください。
この記事を書こうと思ったきっかけは、統計学が重要であるという認識が広まっている一方で、この世の中にあふれている集計結果には検定されずに公表されているものが多い印象を受けたからです。(実際、公表資料に記載されていないだけで、裏ではしっかりやっているものも多数あると思いますが。)
標本調査とクロス集計
クロス集計をした結果を解釈する際に、カイ2乗検定を行うことは最低限必要だと思っています。
理由はいくつかあるのですが、『政治の統計分析』という書籍に端的な記載があったので、紹介します。
すでに指摘したように,世論調査は原則,標本調査である.そのため,世論調査のデータで2つの変数の間に関連性があるように見えても,母集団でもそうであるとは必ずしもいえない.(河村和徳:クロスセクショナル統計シリーズ2 政治の統計分析、共立出版株式会社 2015)
調査をする際に、知りたいのは、得られたデータの結果ではなく、その抽出した母集団でどうなっているのかだと思います。
クロス集計した結果だけを見て“関連がありそう!”と判断するのではなく、クロス集計の検定であるカイ2乗検定を行うことが重要だということです。
詳しい計算方法は省きますが、カイ二乗検定の結果、クロス表をどのように解釈することが可能になるのかを見てみましょう。
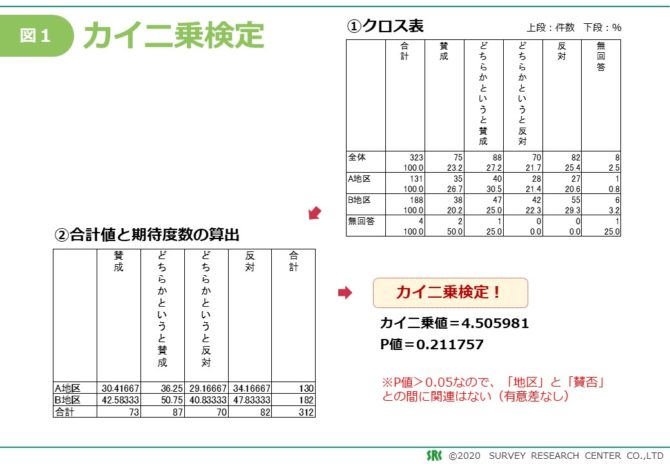
図1をご覧ください。
これは、前回の記事で紹介したクロス表です。(前回の記事『クロス集計は正しく読まなと危ない!~知っておきたいクロス集計の基礎知識①~』はこちら)
これを、カイ2乗検定してみると、p値=0.212となります。
これは、10%水準で考えたとしても、統計的に有意な差があるとは言えない結果です。(p値で統計的な判断をすることに対する議論はここではやりません・・・)
つまり、クロス集計では一見A地区の方が賛成と答える割合が高いように思えますが、統計的にはそうであるとは言えず、地区と賛否の関係には差が見られないということになります。
Excelでカイ二乗検定は大変⁉
ここまでのお話で、標本調査の場合、関連がありそうな調査結果はカイ二乗検定をすることが重要だということがわかってもらえたと思います。
しかし、いざ、エクセルでカイ2乗検定をしようとするとなかなか大変です。
t検定はエクセルのデータ分析ツールで簡単にできますし、回帰分析も制限はありますが分析ツールでできちゃいます。
カイ2乗検定は僕が知る限り、頑張ってExcelで計算式見ながらやるしかないのが現状です(もし、既にできる機能が実装されていたら申し訳ありません・・・)。
集計表の範囲指定とか色々複雑だからカイ2乗検定の簡単なツールは実装されていないような気がしています。
R等の統計分析ツールを使ってカイ二乗検定をした方が早いですし、統計分析ツールが使えない、手間をかけたくないという方は、委託することをおすすめします(その際は、是非弊社まで!)。
この記事を書いた人

田原 歩
最強の男