関係があるように見えるだけ？　〜知っておきたいクロス集計の基礎知識③〜

2020.12.03

こんにちは、ライターの田原です。
２回でネタ切れ！ということもなく、クロス集計で知っておきたいことシリーズは３回目に突入しました。
４回、５回とやっていきたいほど、このクロス集計に関しては色々な課題があると思っています。
「３回目になると内容薄いな」と言われないように頑張ります。

疑似相関

今回ご紹介するクロス集計結果を見る際に気を付けたいことは疑似相関です。
よく、統計における数字のマジックみたいなので使われるネタですね。

疑似相関をインターネットで検索すれば無限と出てくるのですが、今回は僕が統計の研修をするときにいつも使っているものを紹介します。
※弊社は統計の研修もしています。リンク先の記事をご参照ください。
※研修についてのお問い合わせはこちらまで。

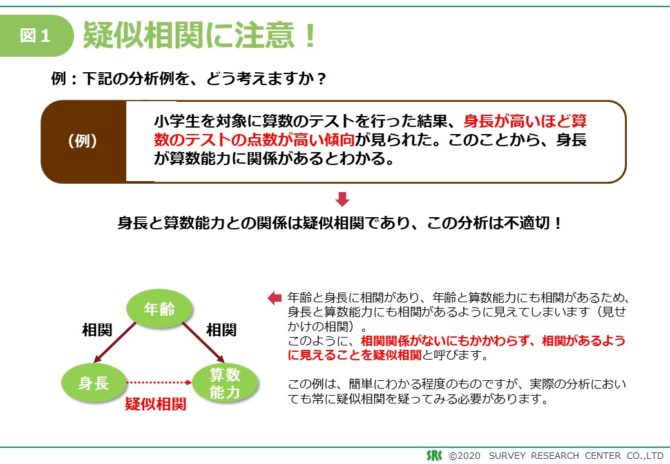
” 小学生を対象に算数のテストを行った結果、身長が高いほど算数のテストの点数が高い傾向が見られた。ここから身長が算数能力に関係があるとわかる。”

もし、こういう分析結果が書かれていたら皆さんどう思いますか。
これは完全におかしな解釈ですね。
わかりやすく図を示すと以下のようになります。

この解釈は、年齢という要素を見落としていたことが問題です。
年齢が高い方が算数能力が高い、もっとわかりやすく言うと、小学校１年生と小学校６年生とでは、小学校６年生の方が算数の問題を解く能力が高いということになります。
当たり前の話ですね。

このように、年齢と身長に相関があり、年齢と算数能力にも相関があるため、身長と算数能力にも相関があるように見えることを疑似相関と呼びます。

さらっと書きましたが、この疑似相関はとても重要です。
クロス集計では、２変数の関係をみることが多いです。
３重クロス、４重クロスをすることもないとは言い切れないですが、一般的な意識調査ではサンプルサイズの関係であまりやりません。
クロス集計は常に疑似相関の可能性があると言えます。

こんなの誰でもわかるよという方もいるとは思いますが、今回はとても簡単なわかりやすい例だから分かっただけです。
全ての疑似相関に気付くことは不可能だと思います。

今回一番言いたかったことは、クロス集計の結果を信用しすぎてはいけないということです。
クロス集計は分析を行う上での基礎であり、きっかけとなりますが、常に第３、第４の変数の影響があるのではないかということを念頭に置いて、そこから統計的な分析を行っていくことが重要ですね。

最強の男